令和2年度　青森県教員採用試験

中学校・高等学校「数学」　解答・解説

1 \(a\)を定数とする。\(x\)の2次関数\(y=x^2-2(a+1)x+5a+3 (0≦x≦2)\)のとき,次の(1)～(3)に答えなさい。

　　(1)この関数のグラフの頂点を求めなさい。

　　(2)この関数の最小値を求めなさい。

　　(3)この関数の最小値が2のとき、\(a\)の値を求めなさい。

2 不等式\(x-3y+6≦0\),　\(3x+y-12≦0\),　\(x+2y-4\)を満たす座標平面上の点\((x,y)\)全体からなる領域を\(D\)とする。
　次の(1),(2)に答えなさい。

　　(1)領域\(D\)を図示しなさい。

　　(2)点\((x,y)\)が領域\(D\)内を動くとき,\(x^2+y^2\)の最大値,最小値およびそのときの\(x,y\)の値を求めなさい。

3 次の(1),(2)に答えなさい。

　　(1)1～9の番号が1つずつかかれた9個の球がある。次の①～③に答えなさい。

　　　　①9個の球を4個,3個,2個の3つのグループに分ける方法は何通りか,求めなさい。
　　　　
　　　　②9個の球を3個ずつ3つのグループに分ける方法は何通りか,求めなさい。
　　　　
　　　　③9個の球をA,B,Cの3つのグループに分ける方法は何通りか,求めなさい。
　　　　　ただし,それぞれのグループに少なくとも1個の球を分けることとする。

　　(2)区別しない9個の球をD,E,Fの3つのグループに分ける方法は何通りか,求めなさい。
　　　　ただし,球を1個も分けてもらえないグループがあってよいものとする。

4 次の(1),(2)に答えなさい。

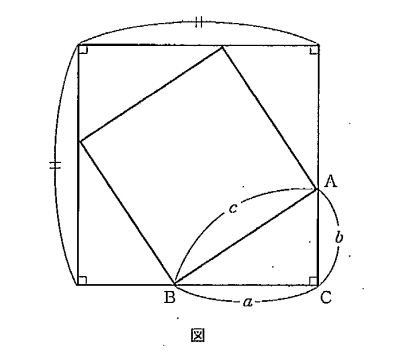
　　(1)図は,直角三角形\(ABC\)と合同な直角三角形を1辺の長さが\(c\)である正方形のまわりにかいたものである。
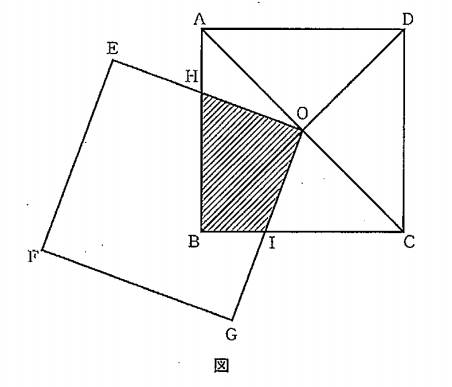
　　　この図を利用して、三平方の定理\(a^2+b^2=c^2\)が成立することを証明しなさい。

　　(2)図のような四角形\(ABCD\)と四角形\(EFGO\)は,1辺が\(6cm\)の合同な正方形であり,点\(O\)は対角線\(AC\),\(BD\)の交点で
　　　ある。2つの正方形が重なった部分(四角形\(HBIO\))の面積が\(9cm^2\)になることを説明しなさい。

5 研究センター前から運動公園前までのバスのルートは,Aルート,Bルート,Cルートの3つがある。次の(1),(2)に答えなさい。

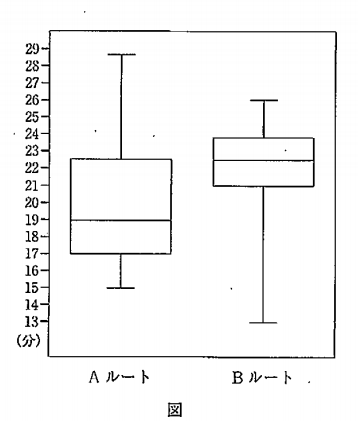
　　(1)図は,Aルート,Bルートをそれぞれ20回運行したときの移動時間の数値を整理した箱ひげ図である。
　　　次の①,②に答えなさい。

　　　　①Aルートの移動時間の数値22分があるとき,Aルートの移動時間のデータの中で,22分は第2四分位数より小さい数値と
　　　　　と大きい数値のいずれになるか,理由を付けて答えなさい。
　　　　
　　　　②AルートとBルートの移動時間のデータを比較したとき,移動時間が20分以上の数値は,AルートとBルートのどちらが
　　　　　多いか,理由を付けて答えなさい。

　　(2)Cルートを利用して5回移動したときの移動時間は,18分,21分,31分,28分,17分となった。次の①,②に答えなさい。

　　　　①この5回の移動時間の平均値,四分位範囲をそれぞれ求めなさい。
　　　　
　　　　②この5回の移動時間の数値のうち1個が誤りであることが分かった。正しい数値に基づく中央値と平均値は,それぞれ
　　　　　22分と24分であるという。誤っている数値を選び、正しい数値を求めなさい。

6 次の文は、新中学校学習指導要領(平成29年度告示)「数学」の「各学年の目標及び内容」の「第3学年」の「目標」である。
　下の(1),(2)に答えなさい。

(1)　数の平方根,多項式と二次方程式,図形の相似,円周角と中心角の関係,三平方の定理,関数\(y=ax^2\),標本調査などについての基礎的な概念や原理・法則などを理解するとともに,事象を(　①　)したり,数学的に解釈したり,数学的に表現・処理したりする(　②　)を身に付けるようにする。

(2)　数の範囲に着目し,_a数の性質や計算について考察したり,文字を用いて数量の関係や法則などを考察したりする力,図　形の構成要素の関係に着目し,図形の性質や計量について論理的に考察し表現する力,関数関係に着目し,その特徴を表, 　式,グラフを相互に関連付けて考察する力,(　③　)と母集団の関係について着目し,母集団の傾向を推定し判断したり, 　調査の方法や結果を(　④　)に考察したりする力を養う。

(3)　(　⑤　)の楽しさや数学のよさを実感して粘り強く考え,数学を生活や学習に生かそうとする態度,問題解決の過程　を振り返って評価・改善しようとする態度,多様な考え方を認め,よりよく問題解決しようとする態度を養う。

　(1)①～⑤にあてはまる語句を書きなさい。
　
　
　(2)中学校第3学年の生徒に対して,下線部aのような力を身に付けさせるために,次に示す学習課題を提示して授業を行った。
　　下の①,②に答えなさい。

学習課題
　2つの連続する偶数の大きい方の2乗から小さい方の2乗を引いた差が偶数になることを,文字を用いた式を使って説明しよう。

　①　この学習課題の解答例を1つ書きなさい。
　
　②　この学習課題解決後,生徒Aから「2つの連続する偶数の大きい方の2乗から小さい方の2乗を引いた差は偶数になるだけでなく,
　　他にも言えることがある。」と発表があった。生徒Aの考えとして予想されることを1つとりあげ,文字を用いた式を使って説明しない。