• (1)


• 


• 　　　　上図より,大きい正方形の面積\(S\)を二通りで表す。
  　　　　
  　　　　\(①\)
  　　　　　　大きい正方形の一辺の長さは,\(a+b\)で表すことができる。
  　　　　　　つまり　　\(S=(a+b)^2\)　　と表すことができる。
  　　　　　
  　　　　　
  　　　　\(②\)
  　　　　　　中にある正方形の面積\(s_1\)と周りにある直角三角形の面積\(s_2\)を足す。
  　　　　　　
  　　　　　　　　　中にある正方形の一辺は\(c\)である。
  　　　　　　　　　よって,　　\(s_1=c^2\)
  　　　　　　　　　
  　　　　　　　　　\(s_2 = \triangle ABC\)の面積 \( \times 4\)　となるので
  　　　　　　　　　\(s_2 = \cfrac{1}{2} a b \times 4\)
  　　　　　　　　　　　\(=2ab\)
  　　　　　　　　　　　
  　　　　　　　　　\(s_1+s_2=c^2+2ab\)
  　　　　　　　　　　　
  　　　　　　つまり　　\(S=c^2+2ab\)　　と表すことができる。
  　　　　　　
  　　　　　　\(①,②\)より
  　　　　　　　　　
  　　　　　　　　　\((a+b)^2 = c^2+2ab\)
  　　　　　　　　　\(a^2 + 2ab + b^2 = c^2 +2ab\)
  　　　　　　　　　\(a^2 + b^2 = c^2\)
  　　　　　　　　　
  　　　　　　よって,三平方の定理\(a^2+b^2=c^2\)が成立する。




• (2)
• 

　　
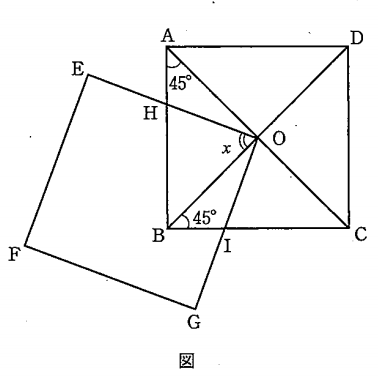
　　　　図より,まず,\(\triangle AHO \equiv \triangle BIO\)を示す。
　　　　
　　　　　　\(\angle HOB = x \)とする。
　　　　　　
　　　　　　\(\angle AOH = \angle BOI = 90^{\circ}-x　―③\)
　　　　　　
　　　　　　\(AO = BO　―④\)
　　　　　　
　　　　　　\(\angle HAO = \angle IBO = 45^{\circ}　―⑤\)
　　　　　　
　　　　\(③～⑤\)より,1組の辺とその両端の角がそれぞれ等しいので
　　　　
　　　　　　\(\triangle AHO \equiv \triangle BIO \)
　　　　
　　　　
　　　　これより
　　　　
　　　　　　(四角形\(HBIO\)の面積)
　　　　　　
　　　　　　　　\(=\triangle HBO + \triangle BIO\)
　　　　　　　　
　　　　　　　　\(=\triangle HBO + \triangle AHO\)
　　　　　　　　
　　　　　　　　\(=\triangle ABO\)
　　　　　　　　
　　　　　　つまり,四角形\(HBIO\)の面積と,\( \triangle ABO\)の面積は等しいので,\( \triangle ABO \)の面積を求めればよい。
　　　　　　
　　　　　　　　\(\triangle ABO = 6 \times 6 \times \cfrac{1}{4} = 9cm^2\)
　　　　
　　　　となる。
戻る